Javascript required
Skip to content Skip to sidebar Skip to footer
Home / Finding General Solution to Differential Equations in Matlab

Finding General Solution to Differential Equations in Matlab

Using Matlab for First Order ODEs

Contents

@-functions
Direction fields
Numerical solution of initial value problems
Plotting the solution
Combining direction field and solution curves
Finding numerical values at given t values
Symbolic solution of ODEs
Finding the general solution
Solving initial value problems
Plotting the solution
Finding numerical values at given t values
Symbolic solutions: Dealing with solutions in implicit form

@-functions

You can define a function in Matlab using the @-syntax:

g = @(x) sin(x)*x

defines the function g(x) = sin(x)·x. You can then
  • evaluate the function for a given x-value:
    g(0.3)
  • plot the graph of the function over an interval:
    ezplot(g,[0,20])
  • find a zero of the function near an initial guess:
    fzero(g,3)

You can also define @-functions of several variables:

G = @(x,y) x^4 + y^4 - 4*(x^2+y^2) + 4

defines the function G(x,y) = x4 + y4 - 4(x2 + y2) + 4 of two variables. You can then

  • evaluate the function for given values of x,y:
    G(1,2)
  • plot the graph of the function as a surface over a rectangle in the x,y plane:
    ezsurf(G,[-2,2,-2,2])
    Click on in the figure toolbar, then you can rotate the graph by dragging with the mouse.
  • plot the curves where G(x,y)=0 in a rectangle in the x,y plane:
    ezplot(G,[-2,2,-2,2])
  • make a contour plot of the function for a rectangle in the x,y plane:
    ezcontour(G,[-2,2,-2,2]); colorbar

Direction Fields

First download the file dirfield.m and put it in the same directory as your other m-files for the homework.

Define an @-function f of two variables t, y corresponding to the right hand side of the differential equation y'(t) = f(t,y(t)). E.g., for the differential equation y'(t) = t y 2 define

f = @(t,y) t*y^2

You must use @(t,y)..., even if t or y does not occur in your formula.
E.g., for the ODE y'=y2 you would use f=@(t,y)y^2

To plot the direction field for t going from t0 to t1 with a spacing of dt and y going from y0 to y1 with a spacing of dy use dirfield(f,t0:dt:t1,y0:dy:y1) . E.g., for t and y between -2 and 2 with a spacing of 0.2 type

dirfield(f,-2:0.2:2,-2:0.2:2)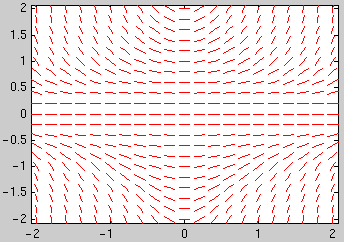

Solving an initial value problem numerically

First define the @-function f corresponding to the right hand side of the differential equation y'(t) = f(t,y(t)). E.g., for the differential equation y'(t) = t y 2 define

f = @(t,y) t*y^2

To plot the numerical solution of an initial value problem: For the initial condition y(t0)=y0 you can plot the solution for t going from t0 to t1 using ode45(f,[t0,t1],y0) .

Example: To plot the solution of the initial value problem y'(t) = t y 2, y(-2)=1 in the interval [-2,2] use

[ts,ys] = ode45(f,[-2,2],1)
plot(ts,ys,'o-')

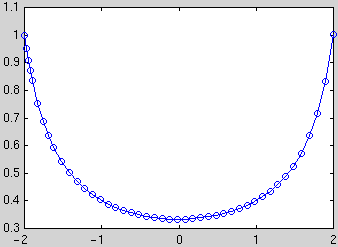
The circles mark the values which were actually computed (the points are chosen by Matlab to optimize accuracy and efficiency). The vectors ts and ys contain the coordinates of these points, to see them as a table type [ts,ys]

You can plot the solution without the circles using plot(ts,ys) .

To combine plots of the direction field and several solution curves use the commands hold on and hold off : After obtaining the first plot type hold on, then all subsequent commands plot in the same window. After the last plot command type hold off.

Example: Plot the direction field and the 13 solution curves with the initial conditions y(-2) = -0.4, -0.2, ..., 1.8, 2:

dirfield(f,-2:0.2:2,-2:0.2:2) hold on  for y0=-0.4:0.2:2    [ts,ys] = ode45(f,[-2,2],y0); plot(ts,ys)  end  hold off

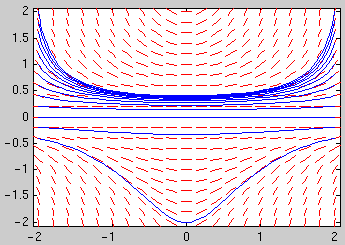
To obtain numerical values of the solution at certain t values: You can specify a vector tv of t values and use [ts,ys] = ode45(g,tv,y0) . The first element of the vector tv is the initial t value; the vector tv must have at least 3 elements. E.g., to obtain the solution with the initial condition y(-2)=1 at t = -2, -1.5, ..., 1.5, 2 and display the results as a table with two columns, use

[ts,ys]=ode45(f,-2:0.5:2,1);
[ts,ys]

To obtain the numerical value of the solution at the final t-value use ys(end) .

It may happen that the solution does not exist on the whole interval:

f = @(t,y) t*y^2
[ts,ys] = ode45(f,[0,2],2);
In this case ode45 prints a warning "Failure at t=..." to show where it stopped.

Note that in some cases ode15s performs better than ode45. This happens for so-called stiff problems. ode15s is also better at detecting where a solution stops to exist if the slope becomes infinite.

Solving a differential equation symbolically

You have to specify the differential equation in a string, using Dy for y'(t) and y for y(t): E.g., for the differential equation y'(t) = t y 2 type

sol = dsolve('Dy=t*y^2','t')

The last argument 't' is the name of the independent variable. Do not type y(t) instead of y.

If Matlab can't find a solution it will return an empty symbol. If Matlab finds several solutions it returns a vector of solutions.

Here there are two solutions and Matlab returns a vector sol with two components: sol(1) is 0 and sol(2) is -1/(t^2/2 + C3) with an arbitrary constant C3.

The solution will contain a constant C3 (or C4,C5 etc.). You can substitute values for the constant using subs(sol,'C3',value) . E.g., to set C3 in sol(2) to 5 use

subs(sol(2),'C3',5)

To solve an initial value problem additionally specify an initial condition:

sol = dsolve('Dy=t*y^2','y(-2)=1','t')

To plot the solution use ezplot(sol,[t0,t1]) . Here is an example for plotting the solution curve with the initial conditions y(-2) = -0.4:

sol = dsolve('Dy=t*y^2','y(-2)=-0.4','t') ezplot( sol , [-2 2])

To obtain numerical values at one or more t values use subs(sol,'t',tval) and double (or vpa for more digits):

sol = dsolve('Dy=t*y^2','y(-2)=1','t')

This gives a numerical value of the solution at t=0.5:

double( subs(sol,'t',0.5) )

This computes numerical values of the solution at t=-2, -1.5, ..., 2 and displays the result as a table with two columns:

tval = (-2:0.5:2)'; % column vector with t-values
yval = double( subs(sol,'t',tval) )% column vector with y-values
[tval,yval] % display 2 columns together

Symbolic solutions: Dealing with solutions in implicit form

Often dsolve says 'Explicit solution could not be found'. But in many cases one can still obtain the solution in implicit form, and use this to plot the graph of the solution, or to obtain numerical approximations.

If dsolve says 'Explicit solution could not be found' there are two possibilities: (Note that different versions of the symbolic toolbox behave differently)

  1. dsolve returns the answer in the form RootOf(expression,z) or solve(equation,y)
    Example 1: Solve the IVP y'=t/(y4-1), y(1)=0.
    dsolve('Dy=t/(y^4-1),y(1)=0','t')
    returns in Matlab R2010b
    RootOf(X89^5 - 5*X89 - (5*t^2)/2 + 5/2, X89)
    This means that the solution in implicit form is
    y5 - 5y - 5t2/2 + 5/2 = 0
  2. dsolve returns the answer [ empty sym ]
    In this case Matlab was unable to find the solution in implicit form. In older versions (e.g. Matlab R2010b) this can even happen when it easy to find by hand the solution in implicit form. In some cases omitting the initial condition helps:
    For Example 1 newer Matlab versions (R2011b, R2012b) return [empty sym]. In this case using dsolve('Dy=t/(y^4-1)','t') gives the implicit solution with a constant. We can then find the value of the constant using the initial condition.
Plotting the solution of IVP in implicit form: If the solution in implicit form is expression=0 use
ezplot(expression,[ tmin tmax ymin ymin ])
to plot the solution y(t) for tmin ≤ t ≤ tmax, ymin ≤ y ≤ ymax.
E.g., for Example 1 we can plot the initial point together with the solution curve by
hold on; plot(1,0,'o');
ezplot('y^5 - 5*y + 5/2 - 5*t^2/2',[-2 2 -2 2]); grid on; hold off

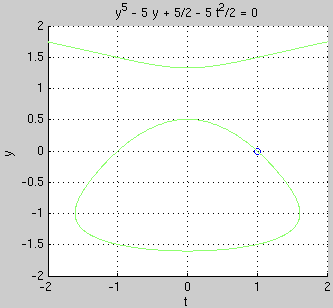
We see from the graph that the interval where the solution exists is roughly (-1.6, 1.6).

Plotting the general solution in implicit form: If the general solution in implicit form is expression=C with C arbitrary, use
ezcontour(expression,[ tmin tmax ymin ymin ])
E.g., for Example 1 we can plot the general solution by
ezcontour('y^5 - 5*y + 5/2 - 5*t^2/2',[-2 2 -2 2])
ezcontour plots contours for 9 values of C. If you want to see more contour curves: Download the file ezcontourc.m and put it in the same directory as your other m-files. Then you can use e.g.
ezcontourc('y^5 - 5*y + 5/2 - 5*t^2/2',[-2 2 -2 2],50)
to obtain contour curves for 50 values of C.

Finding values of the solution in implicit form:
For Example 1 we obtained the solution in implicit form y5 - 5y + 5/2 - 5t2/2 = 0.
We now want to find y(1.5): We plug t=1.5 into the equation and need to solve the equation y5 - 5y + 5/2 - 5·1.52/2 = 0 for y. From the graph above we can see that there are actually 3 solutions: near -1.5, near -0.5, and near 1.5. The solution we want is the one near -0.5.

To find a solution y near -0.5 use
   t=1.5; fzero(@(y)y^5-5*y+5/2-5*t^2/2,-0.5)
which returns the answer y=-0.647819.

Tobias von Petersdorff

Finding General Solution to Differential Equations in Matlab

Source: https://www.grace.umd.edu/~petersd/246/matlabode.html